El artículo del blog de Pinnacle “Una comparación de apuestas niveladas y de porcentajes”, escrito por Joseph Buchdahl (@12Xpert) muestra la importancia de elegir una estrategia para la elección del tamaño de apuesta o stake, y su influencia en el beneficio, yield y probabilidad de estar en pérdidas, tras la realicación de simulaciones Monte Carlo de series de 1000 apuestas.

Este artículo es muy interesante y sirve para aprender sobre la influencia del tamaño de apuesta en los resultados de un método de valor esperado positivo.

La manera de presentar los resultados es muy clara, de modo que he usado el mismo formato de tablas. Sin embargo, las estadísticas de beneficio, yield y probabilidad de estar en pérdidas no son suficientes, en mi opinión, para comparar diferentes estrategias de apuesta.

Desde mi punto de vista, es siempre necesario saber más sobre el riesgo asumido, de modo que el método de apuesta sea aceptable en cuanto a la relación entre beneficio y riesgo.

Al tener en cuenta el riesgo, he llegado a la conclusión de que el criterio de Kelly puro directamente no es viable cuando se aplica stake plano, y también es muy arriesgado para stake proporcional a la banca, o stake porcentual.

Aplicar un factor de reducción al criterio de Kelly (también llamado «Kelly fraccional») es una solución de compromiso que mejora los resultados significativamente. Además, he empleado las simulaciones de Monte Carlo con un número de apuestas superior a 1000.

A menos que se nos proponga jugar al juego de San Petersburgo (una paradoja que consiste en un juego con un Valor Esperado teórico infinito aunque no parezca muy rentable jugar), los apostadores deberían intentar maximizar la relación entre beneficio y riesgo.

Sin embargo, un beneficio esperado muy alto implica probablemente asumir un riesgo siempre mayor que el deseado: «Quien no arriesga, no gana». Pero, al menos, los apostadores pueden decidir cuál es el riesgo que están dispuestos a aceptar y entonces elegir el tamaño de apuesta más apropiado, dependiendo del Valor Esperado, la cuota promedio de las apuestas y el número de apuestas.

Con este artículo, pretendo mostrar por qué es muy importante tener en cuenta el riesgo, empleando para ello el concepto de Máximo Drawdown, y demostrar que, al menos para las estadísticas de yield, cuota promedio y número de apuestas de WinnerOdds, emplear stake proporcional con el criterio de Kelly fraccional es una opción mucho mejor que stake plano para optimizar la relación beneficio / riesgo.

Resultados previos. Stake Plano vs Stake Proporcional

He reproducido los mísmos cálculos del articulo mencionado con @MATLAB (puedes ver el código al final del artículo), para obtener el yield, media y mediana del beneficio obtenido, y probabilidad de estar en pérdidas tras un número determinado de apuestas, con stake plano y con stake proporcional a la banca, ambos con el tamaño de apuesta correspondiente al criterio de Kelly puro.

Tamaño de apuesta del criterio de Kelly = Banca · Valor esperado / (Cuota-1)

Valor Esperado = Probabilidad · Cuota – 1

Hay otras estrategias como el tamaño de apuesta para beneficio constante, que he explicado en el e-book «Cómo ganar dinero apostando«, por @Miguel_Figueres, pero en este artículo, voy a comparar solamente las estrategias de stake plano y stake proporcional.

A raíz de este artículo, he llegado a las siguientes conclusiones:

• El yield promedio en el caso de stake proporcional es menor que el yield promedio con stake plano. Sin embargo, el volumen total apostado con stake proporcional puede llegar a ser tan alto, ya que la banca crece exponencialmente, que el beneficio promedio puede alcanzar valores enormes.
• El beneficio promedio con stake proporcional y el criterio de Kelly puro (tamaño de apuesta como porcentaje de la banca) es mayor que con stake plano para un mismo tamaño de apuesta (en unidades), debido a que se pueden obtener beneficios altísimos con una probabilidad baja (asimetría de la distribución del beneficio).
• La mediana de beneficio (valor que tiene una probabilidad de ser superado del 50%) con stake plano es igual a la media del beneficio, mientras que la mediana del beneficio en el caso de stake proporcional a la banca es menor que el beneficio medio, también debido a la asimetría de la distribución de beneficio.
• El tiempo (o número de apuestas) necesario para recuperarse tras unas pérdidas es mayor con stake proporcional que con stake plano.

Sin embargo, desde mi punto de vista, se deben tener en cuenta otras estadísticas para elegir la mejor estrategia de tamaño de apuesta. Estas otras variables son:

• Riesgo de bancarrota, máximo drawdown y probabilidad de «abandono»
• Tamaño de apuesta con Kelly fraccional
• Varianza y número de apuestas
• Relación entre beneficio y riesgo

Riesgo de bancarrota, máximo drawdown y probabilidad de «abandono»

Tal y como se explica en el artículo escrito por Joseph Buchdahl, teóricamente, la probabilidad de bancarrota (perder el 100% de la banca inicial) en el caso de stake proporcional a la banca es nula, mientras que el riesgo de bancarrota para stake plano con un tamaño de apuesta equivalente puede llegar a ser importante.

Esta es la probabilidad de bancarrota con stake plano (usando el tamaño de apuesta en unidades correspondiente al criterio de Kelly «puro):

En las tablas de resultados, he usado el color de fuente gris para aquellos pares de «Valor Esperado / cuota» que no son factibles, ya que son muy difíciles de conseguir y mantener para un número elevado de apuestas (>1000 apuestas como mínimo).

El cálculo del máximo drawdown (máxima diferencia entre la banca actual y un máximo previo) en unidades no permitiría la comparación de ambos métodos de tamaño de apuesta, pero sí podemos calcular el máximo drawdown como un porcentaje de pérdidas con respecto al valor máximo previo de banca para ambas estrategias:

Máximo drawdown = Max(1 – Banca actual/Valor máximo previo de banca)

La distribución de máximo drawdown para cada estrategia de tamaño de apuesta se muestra en los siguientes gráficos:

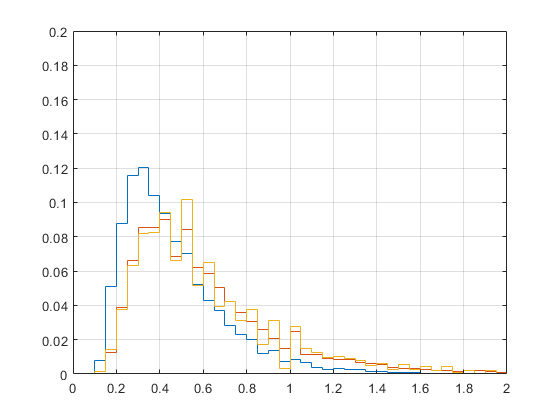
Distribución de máximo drawdown para stake plano (EV=2%(azul) | 5% (rojo) | 10% (naranja), cuota=2.0, anchura de la barra=5%)

Distribución de máximo drawdown para stake proporcional (EV=2%(azul) | 5% (rojo) | 10% (naranja), cuota=2.0, anchura de la barra=5%)

Se puede observar que el máximo drawdown promedio con stake proporcional es mayor, aunque nunca supera el 100%. Esto se debe al hecho de que la relación entre el tamaño de apuesta y la banca se reduce a medida que la banca aumenta (el tamaño de apuesta es constante), mientras que la relación entre tamaño de apuesta y banca con stake proporcional es constante (y el tamaño de apuesta crece a medida que crece la banca). A pesar de ello, el máximo drawdown para stake plano puede superara el 100% de la banca inicial, mientras que el máximo drawdown para stake proporcional es siempre inferior al 100%, y por ello el riesgo de bancarrota con stake proporcional es nulo. Esto hace difícil la comparación de ambas estrategias.

En cambio, podemos considerar la probabilidad de «abandono», asumiendo que un apostador abandonaría el método si en algún momento la banca es inferior al 50% de la banca inicial. Cuando la banca es suficientemente grande como para que el apostador considere que está «apostando los beneficios» en lugar de la banca actual, la tolerancia a mayores valores de máximo drawdown puede ser mayor.

La probabilidad de tener en algún momento una banca inferior al 50% de la banca inicial es mayor en el caso de stake proporcional, sorprendentemente es mayor cuando el valor esperado es grande, ya que también lo es el tamaño de apuesta al aplicar el criterio de Kelly:

Es evidente que, por ejemplo, incluso para un método con un yield o Valor Esperado de 5%, apostar un 5% de la banca a cuota 2 es una estrategia muy arriesgada: Máximos drawdown promedio de 62% y 74% para stake plano y stake proporcional respectivamente, no son bien tolerados en general por los apostadores, incluso teniendo en cuenta los altos beneficios esperados a largo plazo. Usando el mismo ejemplo, la probabilidad de abandono es 36% y 42%, para stake plano y stake proporcional, valores también muy altos.

Estos resultados llevan a la conclusión de que para ambas estrategias de stake, usar el criterio de Kelly puro es demasiado arriesgado y muy pocos apostadores asumirían ese riesgo.

Estrategia con Kelly fraccional

De acuerdo con los resultados previos de máximo drawdown y probabilidad de abandono, parece razonable y precavido emplear un tamaño de apuesta menor. En WinnerOdds usamos un factor de f=0.2 aplicado al tamaño de apuesta calculado a partir del criterio de Kelly puro.

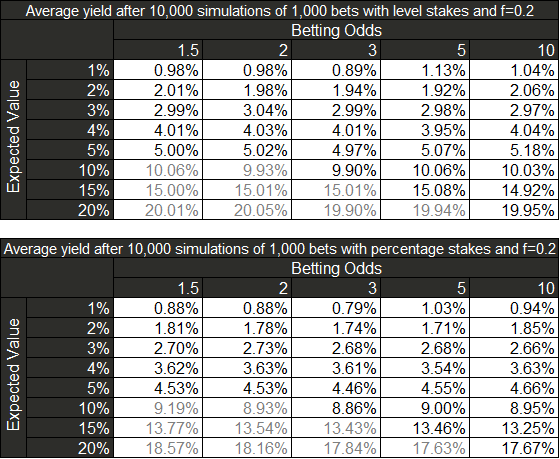
La comparación de resultados obtenida para ambos métodos de stake plano y stake proporcional con tamaño de apuesta según Kelly fraccional muestra una importante mejora de las estadísticas:

• El yield promedio no varía para stake plano, pero el yield de stake proporcional aumenta a valores muy similares a los de stake plano.

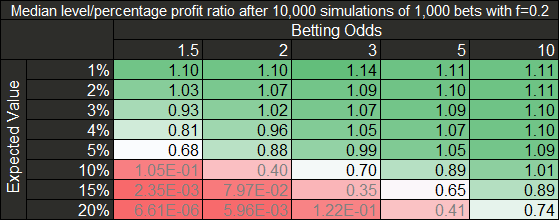
• La relación entre mediana de beneficio de stake plano y stake proporcional se acerca a 1 en todos los casos.

• La probabilidad de estar en pérdidas tras 1000 apuestas no cambia para stake plano, mientras que se reduce para stake proporcional con factor f=0.2 de Kelly fraccional.

• El máximo drawdown promedio se reduce a valores aceptables para ambas estrategias de stake.

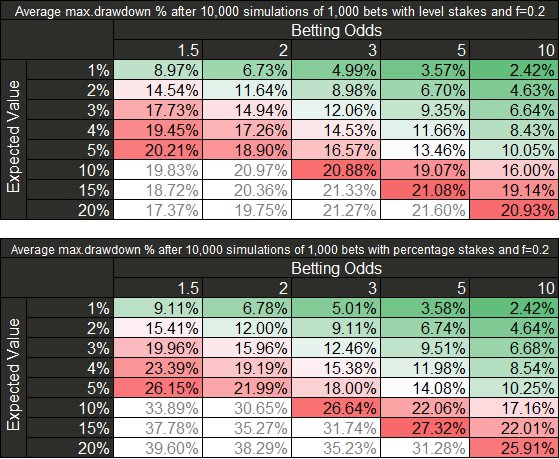
Varianza y número de apuestas

La varianza afecta más significativamente al stake proporcional, debido al hecho de que grandes pérdidas tras varias apuestas consecutivas perdidas requiere de un mayor número de apuestas para recuperar. Además, 1000 apuestas es una muestra relativamente pequeña para cualquier estrategia de apuestas y se puede ver muy influenciada por la varianza en cualquier caso. Con WinnerOdds los usuarios realizan en promedio más de 3000 apuestas al año.

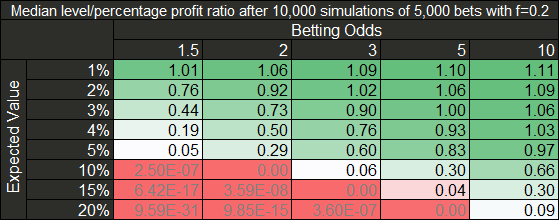
Realizando el análisis para un número de apuestas de 5000, las diferencias en los resultados son:

• El beneficio aumenta exponencialmente para stake proporcional, mientras que lo hace linealmente para stake plano.
• El yield promedio no se ve afectado por el número de apuestas.
• La diferencia entre mediana de beneficio entre stake plano y proporcional se reduce, ya que la mediana de beneficio con stake proporcional aumenta más con el número de apuestas que con stake plano. Solo en el caso de valores muy bajos del cociente “Yield/Cuota promedio”, la mediana de stake plano sigue siendo mayor que la mediana de stake proporcional.

• La probabilidad de estar en pérdidas se reduce al aumentar el número de apuestas con ámbas estrategias de stake, aunque siempre será mayor para el caso de stake proporcional (debido a la asimetría de la distribución del beneficio).

• El máximo drawdown promedio aumenta para ambas estrategias con el número de apuestas, pero con Kelly fraccional (f=0.2) sigue mostrando valores aceptables.

Con un número de apuestas menor que mil, las conclusiones que se podrían obtener irían en el sentido contrario.

La distrubución del máximo drawdown es más razonable para el caso de Kelly fraccional y f=0.2, teniendo en cuenta el número de apuestas de 5.000.

Distribución de máximo drawdown para stake plano (EV=2%(azul) | 5% (rojo) | 10% (naranja), cuota promedio=2.0, f=0.2, anchura de barra=1%)

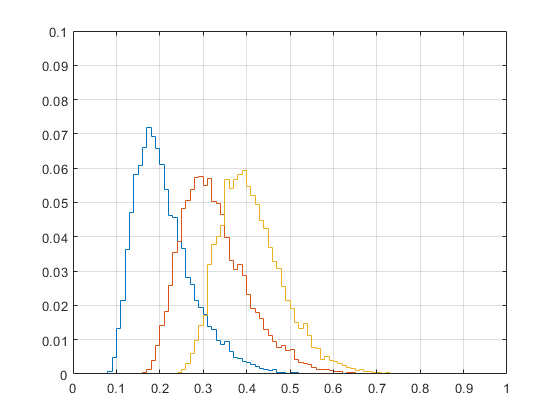
Distribución de máximo drawdown para stake proporcional (EV=2%(azul) | 5% (rojo) | 10% (naranja), cuota promedio=2.0, f=0.2, anchura de barra=1%)

Relación entre beneficio / riesgo

Como apostador, siempre intento optimizar la relación entre beneficio y riesgo. Algunas funciones que se emplean en las carteras de inversiones en bolsa son el ratio de Sharpe, el ratio de Sterling o el ratio de Calmar. En este caso, voy a usar el ratio de beneficio promedio / máximo drawdown promedio como relación entre beneficio y riesgo. Este ratio es similar al ratio de Sterling.

Los resultados para un tamaño de apuesta correspondiente a Kelly fraccional con f=0.2 son:

Se puede observar que en todos los casos, este ratio es superior para la estrategia de stake proporcional.

Conclusiones. Stake Plano o Stake Proporcional

Como resultado de usar la estrategia de Kelly fraccional, y comparar stake plano y stake proporcional, se pueden obtener las siguiente conclusiones:

• Ambas estrategias tiene ventajas y desventajas, dependiendo de la cuota promedio, el Valor Esperado o yield, y el número de apuestas del método de apuestas.
• La varianza afecta más a la estrategia de stake proporcional, si bien el beneficio promedio es mucho mayor.
• La asimetría de la distribución de beneficio hace que la mediana de beneficio sea mayor para stake plano que para stake proporcional, en el caso de métodos con Valor Esperado o yield bajos, cuotas altas y pocas apuestas, mientras que la mediana del beneficio es menor para stake plano que para stake proporcional, en el caso de métodos con Valor Esperado o yield altos, cuota promedio baja y gran número de apuestas, todo ello con la condición del tamaño de apuesta calculado con el criterio de Kelly fraccional.
• Usar Kelly fraccional con f=0.2 hace que el yield, máximo drawdown y la probabilidad de estar en pérdidas tras un determinado número de apuestas del método de stake proporcional se acerquen a los resultados de la estrategia de stake plano, aunque estas estadísticas siempre serán algo mejores para stake plano.
• El ratio entre beneficio promedio y máximo drawdown es siempre más alto para stake proporcional, especialmente para métodos con Valor Esperado alto y cuotas bajas.

Todos estos resultados se resumen en la siguiente tabla:

Los resultados del promedio de usuarios de Winnerodds muestran un yield entre 4% y 5%, con una cuota promedio de 1.5 y un gran número de apuestas, superior a 4.000 apuestas al año. Estas estadísticas hacen que una estrategia de stake proporcional con Kelly fraccional sea claramente mejor que stake plano en este caso.

Si se sigue un método de apuestas que implica un Valor Esperado relativamente bajo, y un número de apuestas bajo o cuotas promedio altas, es posible que emplear stake plano sea una mejor opción.

La simplicidad de usar stake plano es también una ventaja, especialmente cuando el rango de cuotas apostadas es estrecho o el yield no se conoce con mucha precisión (debido a un número de apuestas bajo). Pero en la mayoría de los casos, puede valer la pena (el riesgo) elegir el stake proporcional con Kelly fraccional para optimizar al máximo la relación entre beneficio y riesgo.
Si te ha gustado este contenido, o tienes otras ideas o estrategias, por favor, deja tu comentario. Gracias!

Código

Puedes cambiar los valores y obtener más resultados, usando el siguiente código de @MATLAB. Cualquier mejora, sugerencia o corrección será bienvenida ☺.

yield = [0.01, 0.02, 0.03, 0.04, 0.05, 0.10, 0.15, 0.20];
odds = [3/2, 2, 3, 5, 10];
betsize = 0.05;
nbets = 1000;
mciter = 10000;
bank_ini = 100;
resign = 0.5;
f_kelly = 1;

% Stats
profit_lvl = zeros(length(yield), length(odds), mciter);
yield_lvl = zeros(length(yield), length(odds), mciter);
mu_lvl = zeros(length(yield), length(odds), mciter);
sigma_lvl = zeros(length(yield), length(odds), mciter);
maxdd_lvl = zeros(length(yield), length(odds), mciter);
maxdd_percentage_lvl = zeros(length(yield), length(odds), mciter);
emaxdd_lvl = zeros(length(yield), length(odds), mciter);
resign_lvl = zeros(length(yield), length(odds), mciter);
bankrupt_lvl = zeros(length(yield), length(odds), mciter);
ROI_lvl = zeros(length(yield), length(odds), mciter);
profit_per = zeros(length(yield), length(odds), mciter);
yield_per = zeros(length(yield), length(odds), mciter);
mu_per = zeros(length(yield), length(odds), mciter);
sigma_per = zeros(length(yield), length(odds), mciter);
maxdd_per = zeros(length(yield), length(odds), mciter);
emaxdd_per = zeros(length(yield), length(odds), mciter);
resign_per = zeros(length(yield), length(odds), mciter);
ROI_per = zeros(length(yield), length(odds), mciter);

for i=1:length(yield)
for j=1:length(odds)
disp([‘Yield=’ num2str(yield(i)) ‘ Odds=’ num2str(odds(j))]);
for k = 1:mciter
prob = (1+yield(i))/odds(j);
T = rand(nbets,1)<prob;
betsize = f_kelly*(prob*odds(j)-1)/(odds(j)-1);
% Level stake stats
res = (T*(odds(j)-1)-(1-T))*betsize*bank_ini;
cumres = [bank_ini; bank_ini+cumsum(res)];
maxres = cummax(cumres);
profit_lvl(i,j,k) = sum(res);
yield_lvl(i,j,k) = profit_lvl(i,j,k)/(nbets*betsize*bank_ini);
mu_lvl(i,j,k) = profit_lvl(i,j,k)/nbets;
sigma_lvl(i,j,k) = std(res,0);
emaxdd_lvl(i,j,k) = emaxdrawdown(mu_lvl(i,j,k), sigma_lvl(i,j,k), nbets);
maxdd_lvl(i,j,k) = max(maxres – cumres);
maxdd_percentage_lvl(i,j,k) = 1-min(cumres./maxres);
if any(cumres<bank_ini*(1-resign))
resign_lvl(i,j,k) = 1;
else
resign_lvl(i,j,k) = 0;
end
if any(cumres<0)
bankrupt_lvl(i,j,k) = 1;
else
bankrupt_lvl(i,j,k) = 0;
end
ROI_lvl(i,j,k) = profit_lvl(i,j,k) / bank_ini;
% Percentage stake stats
res = (T*(odds(j)-1)-(1-T))*betsize;
cumres = cumprod([bank_ini; (1+res)]);
cumbet = betsize*cumres;
cumbet = cumbet(1:end-1);
maxres = cummax(cumres);
profit_per(i,j,k) = cumres(end)-bank_ini;
yield_per(i,j,k) = profit_per(i,j,k)/sum(cumbet);
mu_per(i,j,k) = mean(log(1+res));
sigma_per(i,j,k) = std(log(1+res),1);
emaxdd_per(i,j,k) = emaxdrawdown(mu_per(i,j,k), sigma_per(i,j,k), nbets);
maxdd_per(i,j,k) = 1-min(cumres./maxres);
if any(cumres<bank_ini*(1-resign))
resign_per(i,j,k) = 1;
else
resign_per(i,j,k) = 0;
end
ROI_per(i,j,k) = profit_per(i,j,k) / bank_ini;
end
end
end

t{1,1}=(‘Mean Profit (Lvl)’); disp(t{1,1});
t{1,2}=mean(profit_lvl,3); disp(t{1,2});
t{2,1}=’Mean Profit (Per)’; disp(t{2,1});
t{2,2}=mean(profit_per,3); disp(t{2,2});
t{3,1}=’Mean Yield (Lvl)’; disp(t{3,1});
t{3,2}=mean(yield_lvl,3); disp(t{3,2});
t{4,1}=’Mean Yield (Per)’; disp(t{4,1});
t{4,2}=mean(yield_per,3); disp(t{4,2});
t{5,1}=’Median Profit (Lvl)’; disp(t{5,1});
t{5,2}=median(profit_lvl,3); disp(t{5,2});
t{6,1}=’Median Profit (Per)’; disp(t{6,1});
t{6,2}=median(profit_per,3); disp(t{6,2});
t{7,1}=’Median Lvl / Median Per’; disp(t{7,1});
t{7,2}=median(profit_lvl,3)./median(profit_per,3); disp(t{7,2});
t{8,1}=’Prob of non profit Lvl’; disp(t{8,1});
t{8,2}=mean(profit_lvl<0,3); disp(t{8,2});
t{9,1}=’Prob of non profit Per’; disp(t{9,1});
t{9,2}=mean(profit_per<0,3); disp(t{9,2});
t{10,1}=’Probability of bankruptcy Lvl’; disp(t{10,1});
t{10,2}=mean(bankrupt_lvl,3); disp(t{10,2});
t{11,1}=’Mean of resign Lvl’; disp(t{11,1});
t{11,2}=mean(resign_lvl,3); disp(t{11,2});
t{12,1}=’Mean of resign Per’; disp(t{12,1});
t{12,2}=mean(resign_per,3); disp(t{12,2});
t{13,1}=’Mean of MDD Lvl’; disp(t{13,1});
t{13,2}=mean(maxdd_lvl,3); disp(t{13,2});
t{14,1}=’Mean of MDD % Lvl’; disp(t{14,1});
t{14,2}=mean(maxdd_percentage_lvl,3); disp(t{14,2});
t{15,1}=’Mean of EMDD Lvl’; disp(t{15,1});
t{15,2}=mean(emaxdd_lvl,3); disp(t{15,2});
t{16,1}=’Mean of MDD Per’; disp(t{16,1});
t{16,2}=mean(maxdd_per,3); disp(t{16,2});
t{17,1}=’Mean of EMDD Per’; disp(t{17,1});
t{17,2}=mean(emaxdd_per,3); disp(t{17,2});
t{18,1}=’Mean of Profit/MDD Lvl’; disp(t{18,1});
t{18,2}=mean(profit_lvl,3)./mean(maxdd_lvl,3); disp(t{18,2});
t{19,1}=’Mean of Profit/MDD Per’; disp(t{19,1});
t{19,2}=mean(profit_per,3)./mean(maxdd_per*100,3); disp(t{19,2});

% Histogram plots
histogram(maxdd_percentage_lvl(2,2,:),0:0.05:5,’DisplayStyle’,’stairs’,’Normalization’,’probability’); hold on;
histogram(maxdd_percentage_lvl(5,2,:),0:0.05:5,’DisplayStyle’,’stairs’,’Normalization’,’probability’); hold on;
histogram(maxdd_percentage_lvl(6,2,:),0:0.05:5,’DisplayStyle’,’stairs’,’Normalization’,’probability’); hold off;
axis([0 2 0 0.15]); grid;

histogram(maxdd_per(2,2,:),0:0.05:5,’DisplayStyle’,’stairs’,’Normalization’,’probability’); hold on;
histogram(maxdd_per(5,2,:),0:0.05:5,’DisplayStyle’,’stairs’,’Normalization’,’probability’); hold on;
histogram(maxdd_per(6,2,:),0:0.05:5,’DisplayStyle’,’stairs’,’Normalization’,’probability’); hold off;
axis([0 1 0 0.2]); grid;